Binary Search

Binary search is a fast search algorithm with run-time complexity of Ο(log n). This search algorithm works on the principle of divide and conquer. For this algorithm to work properly, the data collection should be in the sorted form.

Binary search looks for a particular item by comparing the middle most item of the collection. If a match occurs, then the index of item is returned. If the middle item is greater than the item, then the item is searched in the sub-array to the left of the middle item. Otherwise, the item is searched for in the sub-array to the right of the middle item. This process continues on the sub-array as well until the size of the subarray reduces to zero.

Problem Statement

Given an array arr[] of n elements in sorted order, write a function to search a given element x in arr[].(Array indexing 0-based, i.e, [0,1,...,n-1] where n is the size of the array). If x is not present in the array return -1.

Solution

Let the given array be

and the number to be searched be 31.

First determine the left and right ends of the array

left = 0 and right = n-1 (here n = 10, the size of array). Thus middle = left + (right - left) / 2 .

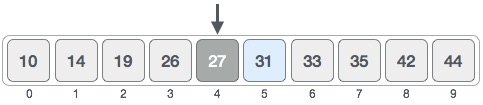
Now, compare the arr[mid] value with x (value to be found). If arr[mid] > x, then we can say x lies to the left of mid. Else if arr[mid] < x, then x lies to the right of mid, else if arr[mid] == x we have found our ans.

Here arr[mid] < 31, thus we change our left = mid+1 and mid = left + (right - left) / 2

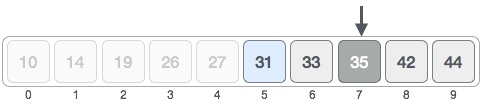
Here arr[mid] > 31, thus we change our right = mid-1 and mid = left + (right - left) / 2

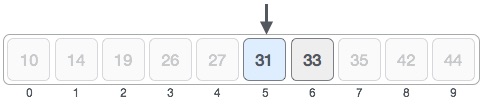
Finally arr[mid] = 31, thus the required pos is mid, where mid = 5

int binarySearch(int arr[],int n, int x){
    int left=0, right=n-1;
    while(left<right){
        int mid=left+(right-left)/2;
        if(arr[mid]>x){
            right=mid-1;
        }
        else if(arr[mid]<x){
            left=mid+1;
        }
        else if(arr[mid]==x){
            return mid;
        }
    }
    return -1; // if x is not present in the array
}

Time Complexity

As mentioned earlier, Binary Search is the fastest algorithm with the time complexity of O(log₂n).

As we keep dividing the array to half it's current size at each iteration, thus the size of the array decreases logarithmically.

At 1st iteration

length = n

At 2nd iteration

length = \( \frac{x}{2} \)

At 3rd iteration

length = \(\frac{x}{2}*\frac{1}{2} = \frac{x}{4}\)

. . .

At k-th iteration

length = \( \frac{n}{2^{k-1}} \)

So, maximum number of interations will be \( \log_2{n} \)

Practice Probelms

Binary Search

Intresting Drink

Books

Know These

upper_ bound:

In-built C++ function, which takes an array or a vector and a value ( say x ) as input and returns a iterator that points to a value just greater than the provided value. ( works on a sorted array / vector ). If there are multiple such values, the one that makes first occurance is returned.

vector<int> v;
int x;
int pos = upper_bound( v.begin() , v.end(), x) - v.begin();

lower_bound:

In-built C++ function, which takes an array or a vector and a value ( say x ) as input and returns an iterator that points to the value not less than the provided value. ( works on a sorted array / vector ). If there are multiple such values, the one that makes first occurance is returned.

vector<int> v;
int x;
int pos = lower_bound( v.begin() , v.end() , x) - v.begin();

If no such value is available, both the functions return an iterator pointing to the end of the array / vector .

Algorithms