Common Backtracking Problems
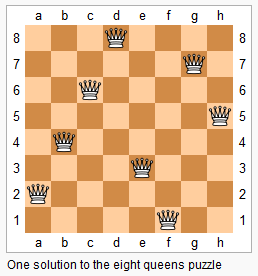
N Queens
Problem Statement:
In a chess game, a Queen can move along 3 axes - horizontal, vertical and diagonal. In this problem, we have an N x N chess board.
Place N Queens on this board in such a way that no two Queens can kill each other (no Queen can reach the position of another Queen in just one move).
Sudoku
Problem Statement:
A sudoku grid is usually a 9 x 9 grid, with some blocks containing a few numbers initially. These numbers fall in the range 1 to 9. A sudoku grid is further divided into 9 3 x 3 subgrids.
We need to fill all the blocks in the grid with numbers from 1 to 9 only, while keeping the following constraints in mind:
-
Each row has only one occurrence of every number from 1 to 9
-
Each column has only one occurrence of every number from 1 to 9
-
Each subgrid has only one occurrence of every number from 1 to 9
A valid sudoku puzzle has a unique solution. However, puzzles with not enough initial values may have more than one valid solution - but these would not be valid sudoku puzzles.
![]()
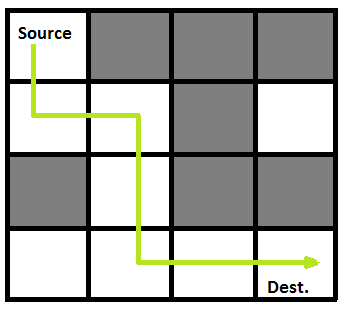
Maze Solver
Problem Statement:
Given a maze, a starting point and a finishing point, write a backtracking algorithm that will find a path from the starting point to the finishing point.
String Permutation
Problem Statement:
Given a string, find all possible permutations that can be generated from it.
Example:
ABC
ACB
BAC
BCA
CAB
CBA
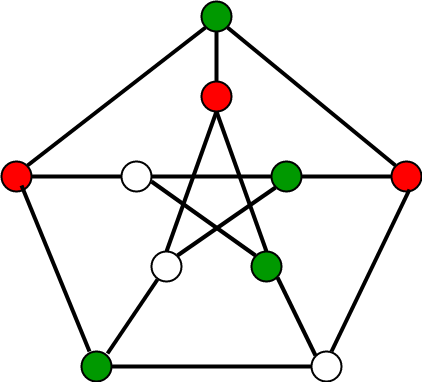
M Colouring
Problem Statement:
Given a graph, find a way to colour every node such that no two connected nodes (nodes which share an edge) are coloured the same and minimum possible number of colours are used.
On a side-but-related note, one might be interested to check out the four colour theorem, proved in 1976.